乗数効果とは何だろうか(初心者向け) 失われた20年の正体(その14)
- 2014/3/31
- 経済
- 1,009 comments

こんにちは、島倉原です。
ここ6回ほどは、日本経済の長期低迷の原因を日銀の金融緩和不足に求める議論を批判的に取り上げつつ、むしろ緊縮財政、即ち財政支出の不足に原因があるのではないか、という問題提起をしてきました。
今後は、財政政策を巡る議論、特に積極財政に反対する議論を取り上げながら、財政政策の有効性を検証していきたいと思います。
今回は、財政支出がGDP拡大に効果を発揮するメカニズムである、「乗数効果」を取り上げたいと思います。
GDPを政府支出以上に拡大、増幅させるのが乗数効果
乗数効果とは、有効需要(金銭的支出の裏付けがある需要。ここでは政府支出)を増加させた時に、当該増加額以上にGDPが増加する現象です。なぜ、このようなことが起こるのでしょうか。
そもそもGDPとは国内の総所得であり、総支出でもあります(誰かの支出は、別の誰かの所得である)。したがって、民間(国内家計及び国内企業)支出(P)と政府支出(G)だけで経済活動が成り立っている国を想定し、その国のGDPをYで表すと、「国内総所得=国内総支出」の関係から、
Y=P+G ~式1
という式が成り立ちます。
ここで、民間部門が全体として、総所得のうちα(ただし、0≦α<1)という割合だけ支出に回すとすると、P=αYとなります。これを式1に代入すると、
Y=αY+G ~式2
となるので、
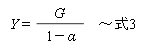
という結果が導き出されます。
つまり、政府が支出を1円増やすと、GDPはその1 / (1-α)倍だけ増える(例えば、民間部門が所得の8割を支出に回すとすると、1 / (1-0.8)=5なので、GDPは5円増える)という訳です。そして1 / (1-α) こそ、「乗数」と呼ばれるものです。
なお、一般的な経済学の教科書では、
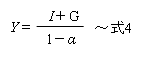
という式が示されていることが通常です(Iは民間部門の投資)。
これは、ケインズが「一般理論」において、αを民間部門(家計)の消費(C)に対してだけ想定し(すなわち、Y=C+I+GかつC=αY)、「社会全体の総投資を1単位増やした時に、総所得がどれだけ増えるか」という観点から乗数効果を論じていることが影響していると思われます。しかしながら、現実の経済では企業の設備投資も所得(企業部門においては利益)の動向に左右されますし、そもそも社会全体の総所得は家計だけでなく企業にも分配される訳ですから、式3のように考える方がしっくり来るのではないかと思います。
乗数効果は「政府の取引先”以外”への波及」によってもたらされる
上記はマクロな観点からの、ある意味で極めて単純化した説明ですが、よりミクロな視点から乗数効果を導くことも可能です。
例えば、政府が新たにX円の公共事業を発注したとしましょう。この場合、建設会社やその下請け企業(資材メーカー、運送業者なども含む)、各社の従業員は全体としてX円の所得を得ることになります。
ここで、所得のうち支出に回す割合がαなので、彼らは全体として新たにαX円の支出を行います。これは、家計としてのモノやサービスへの消費であったり、建設機械への投資であったり、使い道は様々です。その結果、公共事業関係者以外(例えば従業員が買い物をするスーパーや家電量販店、あるいはその従業員)も含めて新たにαX円の所得が生じます。
上記αX円の所得を得た企業や家計は、そのうちのα、すなわちα2X円を支出します。これによってさらに別の誰かがα2X円の所得を得ます。
こうしたプロセスが繰り返されることで、最終的には、
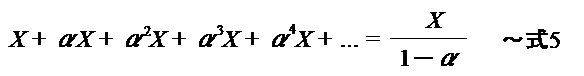
の所得が新たに生まれることになります(式5は等比数列の公式から導き出されます)。これは式3と全く同じ結果であり、乗数はやはり1 / (1-α) です。
上記の説明でも分かるように、公共事業の発生により所得増加の恩恵を得るのは、政府の直接の取引先、あるいはその下請け企業に限りません。彼らの支出先、さらにはそれ以降の波及先は政府支出とはもはや関係なく、幅広い分野で新たな有効需要が生じます。その過程で新たな投資がなされたり、あるいは失業者が雇用されたりすれば、経済全体としての生産力も高まります。
1
2コメント
この記事へのトラックバックはありません。





















この記事へのコメントはありません。