こんにちは、島倉原です。
前回は、

マンデル＝フレミング・モデルを前提とすれば、「変動相場制の開放経済では、金融政策の財政政策に対する『相対的な有効性』が、固定相場制の開放経済の時よりも高くなる」という結論が導き出されるものの、
このこと自体は、一部のリフレ派が「マンデル＝フレミング・モデルの帰結」と称して主張する、「変動為替相場制のもとでは、財政政策よりも金融政策の効果のほうが大きい」という議論の根拠にはならない。

という話をしました。
今回は、

マンデル＝フレミング・モデルを前提とすれば、変動相場制の開放経済では、金融政策の財政政策に対する「相対的な有効性」が、閉鎖経済の時よりも高くなる。

という、前回の話よりもマクロ経済学の教科書で取り上げられることが多い帰結について説明したいと思います。
今回の説明では、「マンキュー　マクロ経済学Ⅰ　入門編」を参考にしています。

右肩下がりとなるIS曲線の成り立ち

マンデル氏の論文の「金利を自由に動かせない」という極端な前提を、「世界第3位の経済大国で、国際的に見ても貿易依存度が低く、経常黒字国で海外資本に頼る必要性にも乏しい国（＝日本）」に当てはめるのは筋違いであることは、前々回述べた通りです。
今回説明するモデルは、マンキューが「アメリカや日本のような国に適用すべき大国開放経済モデル」と述べているものに相当しますが、その前に、基本となる「IS－LMモデル」におけるIS曲線の成り立ちについて触れておきたいと思います。

そもそも、外国との取引を想定しない「閉鎖経済」を前提としたIS－LMモデルでは、一国の経済活動のマクロレベルでのバランスを示すIS曲線を導き出すにあたり、

YE＝C＋I＋G
（YEは国民総支出、Cは民間消費、Iは民間投資、Gは政府支出）

という恒等式を出発点としています。
その上で、

民間消費Cは、国民総所得YIに比例する（比例定数はαとします）。
民間投資Iは、金利rが上昇すると減少する（「何かが上昇すると自身が減少する関係を下向きの矢印↓で表すこととし、I(r↓)と書くことにします）。

という前提を置くことで、

YE＝αYI＋｛I(r↓)＋G｝

という式を導きます。
これは「支出関数」と呼ばれるもので、｛I(r↓)＋G｝の部分は、縦軸にYE、横軸にYIを取った時の支出関数直線（例えば、図1の青い点線）の切片に相当します。この支出関数直線と、「国民総支出＝国民総所得（誰かの支出は、別の誰かの所得である）」というGDPの恒等式を表現した45度線（図1の黒い実線）との交点（図1の黒い点）が、ある金利水準でのGDPの水準を表します。

【図1：閉鎖経済における、金利が上昇した場合の支出関数のシフト

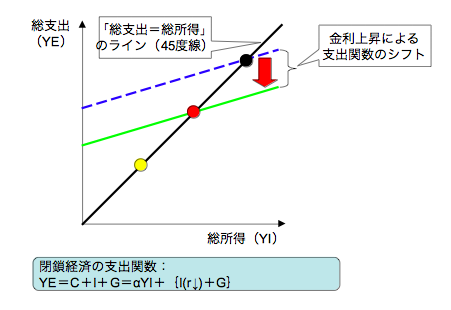
ここで、金利が上昇したとすると、切片が小さくなるため、支出関数直線が下方シフトします（図1の黄緑の実線）。その結果、GDPの水準も図1の赤い点の水準に縮小します。このような「金利が上昇するほど、GDPが縮小する」という関係を、縦軸に金利、横軸に国民所得（GDP）を取って表現すると、右肩下がりの曲線となります。これがIS曲線です。

→ 次ページ「金利変動効果が増幅される開放経済」を読む